GEOMETRİK KAVRAMLAR
Geometride “Nokta”, “Doğru”, “Düzlem” gibi kavramlar tanımsız olarak kabul edilir.
1. Nokta: “.” biçiminde gösterilir. Boyutu yoktur.
2. Doğru: İki uçtan sınırsız noktalar kümesidir.
3. Düzlem: Her yönde sonsuza giden noktalar kümesidir.
E düzlemi dört yönde de sonsuza kadar gider.
 | E düzlemi yandaki gibi gösterilir. |
4. Doğru Parçası : İki nokta ile bu iki nokta arasında kalan noktaların birleşimidir.
[AB] sembolüyle gösterilir.
[AB] : AB doğru parçası
|AB| : AB doğru parçasının uzunluğu
5. Işın : Bir başlangıç noktası olup sonsuza giden noktalar kümesidir.
[AB : AB ışını
6. Yarı Doğru: [AB ışınından A noktasının çıkarılması ile elde edilen kümeye AB yarıdoğrusu denir.
]AB sembolüyle gösterilir.
Doğrusal nokta kümelerinin gösterimi
 | [AB]: A ve B noktaları dahil. |
[AB[: A noktası dahil, B noktası dahil değil | |
]AB[: A ve B noktaları dahil değil |
AÇILAR ;
Başlangıç noktaları ortak iki ışının birleşimine açı denir.
şekilde [AC ve [AB ışınının oluşturduğu açı BAC açısıdır.
[AB gösterilir.[AB ve [AC ışınları açının kenarları, A noktası açının köşesidir. |  |
Açı yazılırken açının köşesi olan nokta ortada yazılır.
1. Açının Ölçüsü
[AB ile [AC arasındaki açıklığın ifadesine açının ölçüsü denir. BAC açısının ölçüsü a dır.m(BAC) = m(A) = | 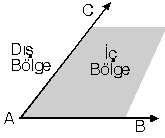 |
è ölçüleri eşit olan açılara eş açılar denir.
2. Açının Düzlemde Ayırdığı Bölgeler
Bir açı düzlemi üç bölgeye ayırır. a. Açının kendisi [AB ve [AC ışınları. b. İç bölge (taralı alan) c. Dış bölge | 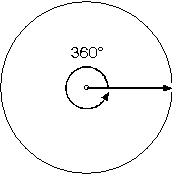 |
3. Açı ölçü birimleri
Açı ölçüsü birimi olarak genelde derece kullanılır. Dereceden başka Grad ve Radyan birimleri de kullanılır. Açı ölçüsü birimleri arasında,
360° = 400 G(grad) = 2 (radyan) eşitliği vardır.
(radyan) eşitliği vardır.
Bir ışının başlangıç noktası etrafında bir tur döndürülmesi ile elde edilen açı 360° dir.
Derecenin alt birimleri
1° = 60' (dakika) 1' = 60" (saniye) 1° = 3600" dir. 90° = 89° 59' 60" ve 180° = 179° 59' 60" olur. | 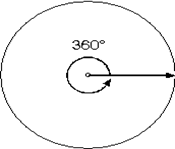 |
4. Ölçülerine göre açılar
a. Ölçüsü 0° ile 90° arasında olan açılara dar açı denir. | 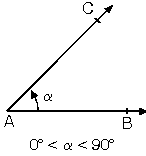 |
b. Ölçüsü 90° olanaçılara dik açı denir |  |
c. Ölçüsü 90° ile 180° arasında olan açılara geniş açı denir. | 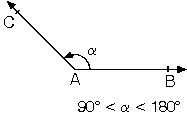 |
d. Ölçüsü 180° olan açılara doğru açı denir. | 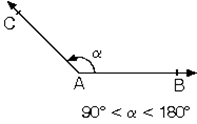 |
e. Ölçüsü 360° olan açıya tam açı denir. |  |
5. Komşu açılar
Köşeleri ve birer ışınları ortak olan, iç bölgesi ortak olmayan açılara komşu açılar denir. CAD ile DAB komşu açılardır. | 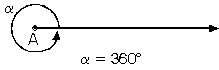 |
6. Açıortay
Açıyı iki eşit parçaya bölen ışına açıortay denir. [AD, CAB açısının açıortayıdır. Açıortay üzerinde alınan her noktanın açının kollarına olan dik uzaklıkları eşittir. | 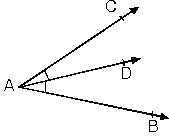 |
7. Tümler açı
Ölçüleri toplamı 90° olan iki açıya tümler açılar denir.
a açısının tümlerinin ölçüsü (90° – a) dır. | 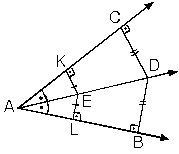 |
Komşu tümler iki açının açıortay doğruları arasındaki açının ülçüsü 45° dir.
 | [OA] [OB] m(KOL) = 45° |
8. Bütünler açı
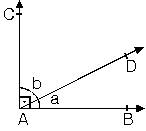
Ölçüleri toplamı 180° olan iki açıya bütünler açılar denir. | 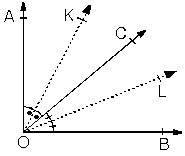 |
m(DAB)+m(CAD)=180° x+y=180° |
x açısının bütünlerinin ölçüsü (180° – x) dir.
Komşu bütünler iki açının açıortay doğruları arasındaki açının ölçüsü 90° dir.
 | m(KOL) = 90° |
9. Ters Açılar
Kesişen iki doğrunun oluşturduğu açılardan komşu olmayanlara ters açılar denir.
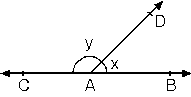 m(x)=m(z) ve m(t)=m(y) dir. | 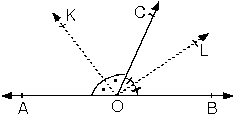 |
10. Paralel iki doğrunun bir kesenle yaptığı açılar
a. Yöndeş açılar
d1 // d2 ise 
|  |
m(a) = m(x) ; m(b) = m(y)
m(c) = m(z) ; m(d) = m(t)
b. İçters açılar
d1 // d2 ise 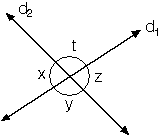 a ile z ve b ile t içters açılarıdır.
m(a) = m(z) ; m(b) = m(t) |  |
Dışters açılar
d1 // d2 ise 
m(c)=m(x)=m(d)=m(y) |  |
d. Karşı durumlu açılar
d1 // d2 ise 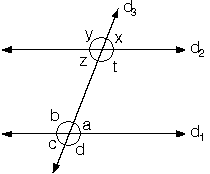
m(a) + m(t) = 180° ; m(b) + m(z) = 180° |  |
Karşı durumlu açıların açıortayları arasındaki açının ölçüsü 90° dir.
Paralel doğrular arasında birden fazla kesenin olduğu durumlarda kesişim noktalarından yeni paraleller çizilir. |
e. Birden fazla kesenli durumlar
d1 // d2 ise B noktasından d1 ve d2 doğrularına paralel çizersek m(ABC) = a + b olur. |  |
B noktasından paralel çizersek m(ABD) + x = 180° m(DBC) + z = 180° buradan x + y + z = 360° dir. | 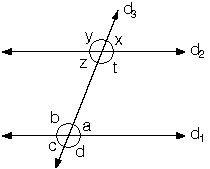 |
f. Paralel doğrular arasındaki ardışık zıt yönlü açılar
d1 // d2 ise a + b + c = x + y olur. Bu tür soruları kırılma noktalarından paraleller çizerek de çözebiliriz. |  |
g. Kolları paralel ve kolları dik açılar
èAçıları oluşturan ışınlar aynı yönde ve paralel ise bu iki açının ölçüsü eşittir. |  |
èAçıları oluşturan ışınlar zıt yönlü ve paralel ise bu iki açının ölçüsü eşittir. | 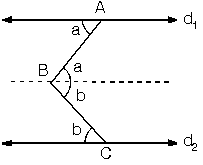 |
èAçıları oluşturan ışınlardan biri aynı diğeri zıt yönlü ve paralel ise bu iki açının ölçüleri toplamı; |  |
èKenarları birbirine dik karşılıklı iki açının ölçüleri toplamı |  |
èKenarları şekildeki gibi birbirine dik açıların ölçüleri eşittir. | 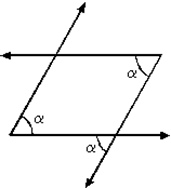 |





0 yorum:
Yorum Gönder